不经意传输 [Oblivious Transfer (OT)]
不经意传输(oblivious transfer)是一个密码学协议,在这个协议中,消息发送者从待发送的消息集合中发送数据给接收者,但事后对发送了哪一条消息仍然oblivious(不知道),同时接受者对自己想要接受外的数据一无所知,这个协议也叫茫然传输协议。
这个文章给出我看的几个不经意传输的论文笔记。
什么是不经意传输
一、不经意传输开山作
不经意传输(Oblivious Transfer, OT)最早由 Rabin 于 1981 年提出,旨在解决双方在秘密交换过程中如何实现结果一致性的问题。在 Rabin 提出的 OT 协议中,发送方 Alice 向接收方 Bob 发送一条消息,Bob 仅有一定概率能够成功接收该消息,并且 Alice 无法获知 Bob 是否实际收到了该消息。该概率是严格可控的,在原始协议设计中为 $50%$。这种“接收方是否成功接收对发送方保持不可知”的特性,正是不经意传输的核心属性。 首先,介绍预备知识如下:
1.1 在模 n 下求二次剩余的问题
- 问题定义
给定一个合数 $n = p \cdot q$【$p,q$ 为不同的大质数】,求 $c$ 的平方根 $x$ 满足 $c \equiv x^2 \pmod n$。
上述问题的求解并不总是容易的,如果知道 $p,q$,那么可以使用 cipolla 或 Tonelli-Shanks 算法以对数复杂度求 $x$。如果不知道 $n$ 的因式分解 $p,q$,那么求解 $x$ 与分解 $n$ 的难度等价。
-
问题简化
我们首先给出求解方程 $c \equiv x^2 \pmod p$ 的方法,其中 $p$ 是一个奇素数。
(1). 使用欧拉判别法判定 $c$ 是否为二次剩余,从而判定是否存在满足条件的 $x$: $$ c^{\frac{p-1}{2}} \equiv \begin{cases} 1 \pmod p, & \text{$c$ 为二次剩余,有解,可继续;}\\ -1 \pmod p, & \text{$c$ 非二次剩余,无解。} \end{cases} $$ (2). 如果通过欧拉判别法确定方程有解,则可判断 $p$ 是否满足特殊条件,若满足可快速计算 $x$。如果 $p \equiv 3 \pmod 4$ 成立,则可以直接求出 $x_1 = a_p \equiv c^{\frac{p+1}{4}} \pmod p$ 和 $x_2 = p - x_1$。
(3). 如果 p 不满足 (2) 中的式子,判断 $p \equiv 5 \pmod 8$ 是否成立,如果成立,则可以按照如下方式计算 $x$:首先计算 $x \equiv c^{\frac{p+3}{8}} \pmod p$,若 $x^2 \equiv c \pmod p$,则 $x_1 = a_p = x$。否则取 $z \equiv 2^{\frac{p-1}{4}} \pmod p$,并求得 $x_1 = a_p \equiv x \cdot z \pmod p$。最终 $x_2 = p -x_1$。
(4) 当 $p$ 不落入 (2)(3) 的快速情形时,可以使用通用算法求解平方根:(4a) Cipolla 算法
- 先做欧拉判别,确认 $c$ 为二次剩余。
- 随机取 $a \in Z_p$,直到 $(a^2 - c)$ 为二次非剩余。 【即 $(a^2 - c)^{(p-1)/2} \equiv -1 \pmod p$】
- 在扩域 $\mathbb{F}_{p^2} = \mathbb{F}_p[\omega]$ 中运算,定义 $\omega^2 \equiv a^2 - c \pmod p$。
- 计算 $(a+\omega)^{\frac{p+1}{2}}$【可用二进制快速幂完成指数运算】,扩域中的乘法规则为
$$ (u+v\omega)(u’+v’\omega) \equiv (uu’ + vv’(a^2-c)) + (uv’ + vu’)\omega \pmod p $$ - 上式的结果必定为 $x + 0\cdot \omega$ 的形式,其中 $x$ 即为平方根之一,另一个为 $p - x$。
(4b) Tonelli–Shanks 算法
- 先做欧拉判别,确认 $c$ 为二次剩余。
- 将 $p-1$ 分解为 $p-1 = Q \cdot 2^S$,其中 $Q$ 为奇数。
- 找到一个二次非剩余 $z$,满足 $z^{\frac{p-1}{2}} \equiv -1 \pmod p$。
- 初始化:$M \leftarrow S$,$c_1 \leftarrow z^Q \bmod p$,$t \leftarrow c^Q \bmod p$,$R \leftarrow c^{\frac{Q+1}{2}} \bmod p$。
- 当 $t \not\equiv 1 \pmod p$ 时: 首先找到最小的 $i \in \{0, \dots, M-1\}$ 使得 $t^{2^i} \equiv 1 \pmod p$ 成立;然后令 $b \leftarrow c_1^{2^{M-i-1}} \bmod p$ 并更新初始化参数为:
$$ R \leftarrow R \cdot b \pmod p,\quad t \leftarrow t \cdot b^2 \pmod p,\quad c_1 \leftarrow b^2 \pmod p,\quad M \leftarrow i $$ - 当 $t \equiv 1 \pmod p$ 时,$R$ 即为平方根之一,另一条为 $p - R$。
- 问题解法
当 $n = p \cdot q$,且 $p, q$ 为不同的大质数时,要求解 $c \equiv x^2 \pmod{n}$,可以利用中国剩余定理将问题分解为两个模素数的平方根求解问题。首先使用已知的 $p,q$ 将原方程拆分为: $$ \begin{cases} x^2 \equiv c \pmod{p} \\ x^2 \equiv c \pmod{q} \end{cases} $$ 接着,对模 $p$ 的方程 $x^2 \equiv c \pmod{p}$,使用问题简化中的方法得到两个解 $r_p$ 与 $p - r_p$。
然后,对模 $q$ 的方程 $x^2 \equiv c \pmod{q}$,同理求解,得到两个解 $r_q$ 与 $q - r_q$。
最后,由于模 $p$ 下有 2 个解,模 $q$ 下也有 2 个解,组合得到 $2 \times 2 = 4$ 组同余方程: $$ \begin{cases} x \equiv r_p \pmod{p} \\ x \equiv r_q \pmod{q} \end{cases} \ \begin{cases} x \equiv r_p \pmod{p} \\ x \equiv -r_q \pmod{q} \end{cases} \ \begin{cases} x \equiv -r_p \pmod{p} \\ x \equiv r_q \pmod{q} \end{cases} \ \begin{cases} x \equiv -r_p \pmod{p} \\ x \equiv -r_q \pmod{q} \end{cases} $$ 用中国剩余定理(CRT)合并每组解即可,以第一组同余为例:
$$ \begin{cases} x \equiv r_p \pmod{p} \\ x \equiv r_q \pmod{q} \end{cases} $$ 解上述方程组可得 $c \equiv x^2 \bmod n$ 的其中一个解为 $x \equiv r_p \cdot m_p + r_q \cdot m_q \pmod{n}$ 。对 4 个方程组使用同样的方法即可得到模 $n$ 下的 4 个平方根。【$m_p,m_q$ 的计算参考CRT计算方式】
注意:当 $n = p \cdot q$ 的质因子未知时,模 $n$ 求平方根的难度与分解 $n$ 的难度等价,该困难问题是许多公钥密码(如 RSA 和 Rabin 加密)的安全基础。简单证明如下:
定理一:设 $n = p \cdot q$($p, q$ 为不同的大质数),且 $c$ 在模 $n$ 下是二次剩余。若 $c \equiv x^2 \pmod{n}$ 的两个平方根 $x, y$ 满足 $x \not\equiv \pm y \ (\bmod\ n)$,则 $p = \gcd(y - x, n),\ q = \gcd(y + x, n)$ 给出了 $n$ 的两个非平凡因子,从而可得到 $n$ 的因式分解 $n = p\cdot q$。
证明:由于 $x$ 和 $y$ 都是 $c$ 的平方根,因此有
$x^2 \equiv c \pmod{n}, \ y^2 \equiv c \pmod{n}$ 成立,也就是等式
$x^2 \equiv y^2 \pmod{n}$ 成立。
因此我们有 $n \mid (y - x)(y + x)$。
因为 $n = p \cdot q$,由整除的性质可知 $p$ 和 $q$ 必然分别整除 $(y-x)$ 或 $(y+x)$ 中的一个。
若 $x \equiv y \ (\bmod\ n)$,则 $y - x$ 可被 $n$ 整除,$\gcd(y-x, n) = n$,无意义;
若 $x \equiv -y \ (\bmod\ n)$,则 $y + x$ 可被 $n$ 整除,$\gcd(y+x, n) = n$,无意义。
但当 $x \not\equiv \pm y \ (\bmod\ n)$ 时,$(y-x)$ 与 $(y+x)$ 中各含有一个质因子,故可得 $n = p\cdot q$ 且:
$$
p = \gcd(y - x, n), \quad q = \gcd(y + x, n)
$$
1.2 Rabin 不经意传输(OT)协议
Rabin 不经意传输(OT)协议的目标是让发送方 Alice 向接收方 Bob 发送一条消息,但 Bob 只有一定概率(本文是1/2)能够获得该消息,并且 Alice 不知道 Bob 是否成功接收到了消息。
Rabin OT协议基于上述介绍的模 n 求平方根的性质(该协议发送的消息是 $p,q$)。协议步骤如下:
- Alice 生成两个大质数 $p, q$,计算 $n = p * q$,将 n 发送给 Bob,自己保留 p, q。
- Bob 选择一个随机数 $x \in Z_n$,计算 $c = x^2 \bmod n$,将 c 发送给 Alice,同时保留 x。
- Alice 用 p, q 计算 c 的四个平方根 $\{±x, ±y\}$(其中 x, y 在模 n 下不同),随机选择其中一个平方根 r 发送给 Bob。
- Bob 知道自己选择的 $x$,因此他可以检查 $r = ±x$ 是否成立:
- 如果 $r \neq ±x$,则 $r$ 和 $x$ 是两个不同的平方根,可以通过定理一分解 n。
- 如果 $r = ±x$,则无法分解 n。
协议性质:
- Bob 成功分解 n 的概率为 1/2,因为 Alice 是从四个平方根 $\{±x, ±y\}$ 中随机选择 $r$ 返回的。
- Alice 不知道 Bob 是否成功分解了 n 。这是因为 Alice 不知道 Bob 选的 x,因此无法判断自己返回的平方根是否与 Bob 已知的相同,也就无法知道 Bob 是否成功分解 n。
- 安全性依赖大数分解困难性:在 Bob 收不到不同平方根时,他无法分解 n。
1.3 Rabin 秘密交换协议(EOS)
Rabin 通过上述构造的 OT 协议构建了一个秘密交换协议。
Alice 有秘密 $S_A$,Bob 有秘密 $S_B$,他们想互相交换自己的秘密,EOS协议协议保证在没有第三方参与的情况下,要么双方都知道对方的秘密,要么双方都不知道。 EOS协议是为了解决一个常见的问题,Alice 收到秘密 $S_B$ 之后,不把自己的秘密 $S_A$ 交给 Bob,导致潜在的问题。
背景与假设
Alice 和 Bob 各自持有一个秘密,分别记为 $S_A$ 和 $S_B$【在下述假设下,不失一般性,设他们只有一比特】,他们希望在没有可信第三方、且不存在安全同步消息交换机制的情况下交换秘密。
例如将秘密视为访问对方某文件的密钥,并假设输入错误密钥会破坏文件,排除暴力猜测的可能。
假设 Bob 使用 $S_A$ 读取 Alice 的文件后,Alice 会知晓这一行为,反之亦然。
在异步通信中,一方可以在获得对方秘密后中止协议,从而单方面获利。为此,需要设计一种协议,使得在任何情况下要么双方同时获得对方的秘密,要么双方都得不到,且任何一方在未释放自己秘密的情况下不能提前获得对方的秘密。
协议步骤
-
一次性密钥的交换
Alice 生成一次性 RSA 模数 $n_A = p \cdot q$(仅 Alice 知道分解),发送给 Bob。
Bob 生成一次性 RSA 模数 $n_B = p_1 \cdot q_1$(仅 Bob 知道分解),发送给 Alice。 -
双向 OT 的概率交换
Bob 作为发送方执行 OT 协议:- Bob 随机选 $x$,计算 $c = x^2 \bmod n_A$,发送 $c$ 给 Alice,同时隐藏 $x$。
- Alice 用 $p, q$ 计算 $c$ 的四个平方根,随机选择一个发送给 Bob。
- Bob 有 $1/2$ 概率得到 $n_A$ 的分解(OT 原理)。
定义 $v_B = 0$ 表示 Bob 得到分解,$v_B = 1$ 表示没得到。
Alice 作为发送方执行 OT(过程相同):
- 随机选 $x$,计算 $c = x^2 \bmod n_B$,发送给 Bob。
- Bob 用 $p_1, q_1$ 计算平方根,随机返回一个给 Alice。
- Alice 有 $1/2$ 概率得到 $n_B$ 的分解。
定义 $v_A$ 类似。
-
隐藏秘密的中间编码
双方暂时不能直接发送秘密,因为此时对方可能还没得到分解。
Bob 计算 $\varepsilon_B = S_B \oplus v_B$ 并签名发送给 Alice。
Alice 计算 $\varepsilon_A = S_A \oplus v_A$ 并签名发送给 Bob。
如果对方知道 $v$,就能立刻还原秘密;如果不知道 $v$,值无用。
重要的是,在此阶段无法单独利用 $\varepsilon$ 获得秘密,因为不知道对方的 $v$。 -
加密秘密的发送
Alice 将 $S_A$ 放入一个随机消息 $m_A$ 中,用 $n_A$ 的公钥加密得到 $d_A = E_{n_A}(m_A)$,发送给 Bob。Bob 将 $S_B$ 以相同方式加密,发送给 Alice。
协议完成后的情况分析
- 如果 $v_A = 0$,说明 Alice 得到了 $n_B$ 的分解,此时它可以计算出RSA解密私钥,从而它可以解密获得 $S_B$;一旦她查看了文件,Bob就知道他成功分解了 $n$,此时Bob知道 $v_A = 0$, 则 Bob 可以计算出 $S_A = \varepsilon_A \oplus v_A$,所以双方都知道秘密。Bob 的情况同理。
- 如果双方都没得到分解,双方都无法解出对方秘密。
- 该协议可以解决秘密交换问题。协议完成后,双方都无法获得对方秘密的概率是 $1/4$。
证明(简述):- 如果在最后阶段前一方中断,另一方也会停止,因此无人能知道对方的秘密。
- 如果 Bob 在最终阶段收到了 $d_A$ 且知道 $n_A$ 的分解($\nu_B = 0$),他可以解密得到 $S_A$ 并读取文件。根据假设,这会让 Alice 知道 Bob 已读取文件,因此 Alice 推出 $\nu_B = 0$,进而 $\varepsilon_B = S_B \oplus 0 = S_B$,获取 $S_B$。同理,如果 Alice 先读取文件,Bob 也能得到 $S_A$。
- 因此,上述协议中任意一方读取文件意味着另一方也能得到对应的秘密从而读取文件,从而保证了秘密交换的原子性。双方都不能分解对方密钥的概率为 $(1/2)^2 = 1/4$。
- 可以改进遗忘传输(OT)子协议:
Bob 在收到 $n_A$ 后选择两个数 $x, y \leq n_A$,发送它们的平方给 Alice。Alice 返回两个平方根。这样 Bob 有 $3/4$ 概率获得 $n_A$ 的分解。改进后:
- 单次遗忘传输失败概率为 $1/4$;协议整体失败概率为 $(1/4)^2 = 1/16$;
- 虽然提高成功概率(例如 $1 - 1/32,000$)能让成功率接近 1,但参与者可能会提前停止并直接使用 $\varepsilon_B$ 作为秘密的动力,因此增强存在上限。
二、二选一不经意传输(1-out-2 Oblivious Transfer)
Even 等人在 1985 年提出了二选一不经意传输协议(1-out-of-2 Oblivious Transfer, $OT_2$),与最初 Rabin 的 OT 协议不同,二选一不经意传输协议的定义如下:
在 $OT_2$ 协议中,发送方 S 持有两个可识别的秘密消息 $M_1$ 和 $M_2$,接收方 R 只能以恰好 1/2 的概率获得其中一个消息(要么是 $M_1$,要么是 $M_2$),且对另一个消息无法获得任何有用的部分信息。同时,发送方在协议执行完毕后不知道接收方获得的是哪一个消息。此外,如果发送方试图作弊以推测接收方选择了哪一个消息,则接收方至少有一半的概率能够检测到这种作弊行为。
2.1 二选一遗忘传输协议
-
本节目标是基于任意满足一定条件的公钥密码系统实现一个符合定义的 OT₂ 协议满足:
(1) 接收方恰好获得两条消息中的一条,另一条无法获得任何有用信息;
(2) 发送方不知道接收方获得的是哪一条;
(3) 如果发送方作弊,接收方至少有 $ \frac12 $ 的概率检测到。 -
首先引入两个运算符 $ \oplus $ 和 $ \ominus $,它们在 PKCS 的消息空间上定义,满足:
- 对任意 $ x $,映射 $ y \mapsto x \oplus y $ 是置换
- 对任意 $ y $,映射 $ x \mapsto x \oplus y $ 是置换
- 对任意 $ x, y $,有 $ (x \ominus y) \oplus y = x $
具体实现时,$ \oplus $ 和 $ \ominus $ 的定义依赖所用的公钥密码系统,例如在 RSA 中可以用模 $ N $ 下的加法与减法,在二进制向量空间中可以用按位异或等。
-
OT₂ 协议的执行过程如下:
-
发送方在公钥密码系统的消息空间中随机生成一对公钥/私钥 $(E, D)$,并随机选择两个不同的消息 $m_0$ 和 $m_1$。这两个消息作为接收方选择的“掩码值”,用于在后续步骤中混合密钥信息。然后,发送方将公钥 $E$ 及这两个随机消息组成的三元组 $(E, m_0, m_1)$ 发送给接收方。
-
接收方收到 $(E, m_0, m_1)$ 后,随机选择一个比特 $r \in \{0, 1\}$ 作为希望接收的消息的索引,并使用公钥 $E$ 加密随机的会话密钥 $k$,得到 $E(k)$。然后计算 $q = E(k) \oplus m_r$ 以隐藏自己选择的索引 $r$,同时保证只有自己能解出对应的真实消息。接收方将 $q$ 发送给发送方。
-
发送方收到 $q$ 后,对每个 $i \in {0, 1}$ 分别计算 $k_i = D(q \ominus m_i)$ 得到两个候选密钥 $k_0$ 和 $k_1$。随后,他计算 $M_0 \oplus k_0$ 和 $M_1 \oplus k_1$,并随机选择一个比特 $s$ 作为额外的随机参数,最后将消息密文 $(M_0 \oplus k_0, M_1 \oplus k_1, s)$ 一并发送给接收者。
-
接收方利用自己选择的 $r$ 及已知的会话密钥 $k$,对收到的密文进行解密,恢复出对应的真实消息 $M_r$。由于缺少另一条消息所需的密钥,接收方无法获得 $M_{1-r}$ 的任何有用信息。
----------------------------------------------------------------------- 发送方 S 接收方 R ----------------------------------------------------------------------- (1) 生成 (E, D), 随机选择 m0, m1 发送 (E, m0, m1) ------------------------------------> (2) 选择 r ∈ {0,1} 生成 k q = E(k) ⊕ m_r 发送 q <--------------------------------- (3) 对 i ∈ {0,1} 计算: k_i = D(q ⊖ m_i) 计算 M0 ⊕ k0, M1 ⊕ k1 选择随机比特 s 发送 (M0 ⊕ k0, M1 ⊕ k1, s) -------------------------------------> (4) 用已知的 r 和 k 解密得到 M_r
-
-
协议性质分析
该 OT₂ 协议能够满足前述三个性质,原因如下:
(1) 接收方恰好获得两条消息中的一条:接收方只能解密出索引 $r$ 对应的消息 $M_r$,因为只有这一条消息的密钥 $k_r$ 是由自己生成的。接收方并不知道另一条消息 $M_{1-r}$ 对应的密钥 $k_{1-r}$,由于公钥密码系统的安全性和 $\oplus$ 运算的性质,即便知道 $M_{1-r} \oplus k_{1-r}$ 也无法高效恢复 $M_{1-r}$,因此接收方无法获得另一条消息 $M_{1-r}$ 的任何有用信息。(2) 发送方不知道接收方获得的是哪一条: 发送方无法区分接收者在步骤二中选择的 $r$ 值是多少,因为 $q = E(k) \oplus m_r$ 对于不同的 $r$ 来说,分布完全相同。在公钥密码系统安全性的保证下,发送方不能通过分析 $q$ 来推断出 $r$ 的信息,因此知道哪条消息被接收的概率仍为 $1/2$。
(3) 发送方作弊可被接收方至少一半概率检测到: 若发送方不按照协议的流程执行,试图构造特殊的消息 $(M_0 \oplus k_0, M_1 \oplus k_1, s)$ 以推测接收方选择了哪条消息,接收方在验证解密结果与预期不符时会发现异常。由于接收方的选择是随机的,发送方至多有 $1/2$ 的概率猜对 $r$ 而不被发现,因此检测概率至少为 $1/2$。
三、n选一不经意传输协议
由于大量基于 OT 的密码协议在执行过程中需要调用海量 OT 实例,因此提升 OT 的计算与通信效率一直是该领域的核心问题之一。2015 年的论文《The Simplest Protocol for Oblivious Transfer》提出了当时最为简洁高效的 n选一不经意传输协议。该协议在计算开销方面表现突出:仅需 2 + 3m 次全指数运算(其中接收方执行 2m 次,发送方执行 2 + m 次),即可完成 m 次 1-out-of-n OT;在通信开销方面,仅需传输 m+1 个群元素和 2mn 个密文。此外,该协议可基于椭圆曲线实现,在保持安全性的同时显著提升性能,为构建高效且可扩展的 OT 协议提供了重要基础。
3.1 协议的原始思路
这篇论文的核心思想源于对Diffie–Hellman (DH)密钥协商协议的观察。 在经典的 DH 协议中:
- Alice 选择随机数 $a$,计算 $A = g^a$,并将 $A$ 发送给 Bob;
- Bob 选择随机数 $b$,计算 $B = g^b$,并将 $B$ 发送给 Alice;
- 双方分别计算共享密钥:Alice 计算 $k = (g^b)^a = g^{ab}$;Bob 计算 $k = (g^a)^b = g^{ab}$。
论文作者注意到,Alice实际上还能从 $(B/A)^a = g^{(b-a)a} = g^{ab-a^2}$ 中导出另一组独立的密钥,而Bob在CDH假设下无法获得该值。 基于这一观察,如果让发送方在 DH 协议中扮演 Alice,接收方扮演 Bob,并将 Bob 的密钥计算方式与其选择位 $c$ 绑定,即可构造一个简单且高效的随机 OT 协议。进一步地,通过使用随机 OT 输出的密钥加密发送方的真实消息,即可得到标准 OT 协议。
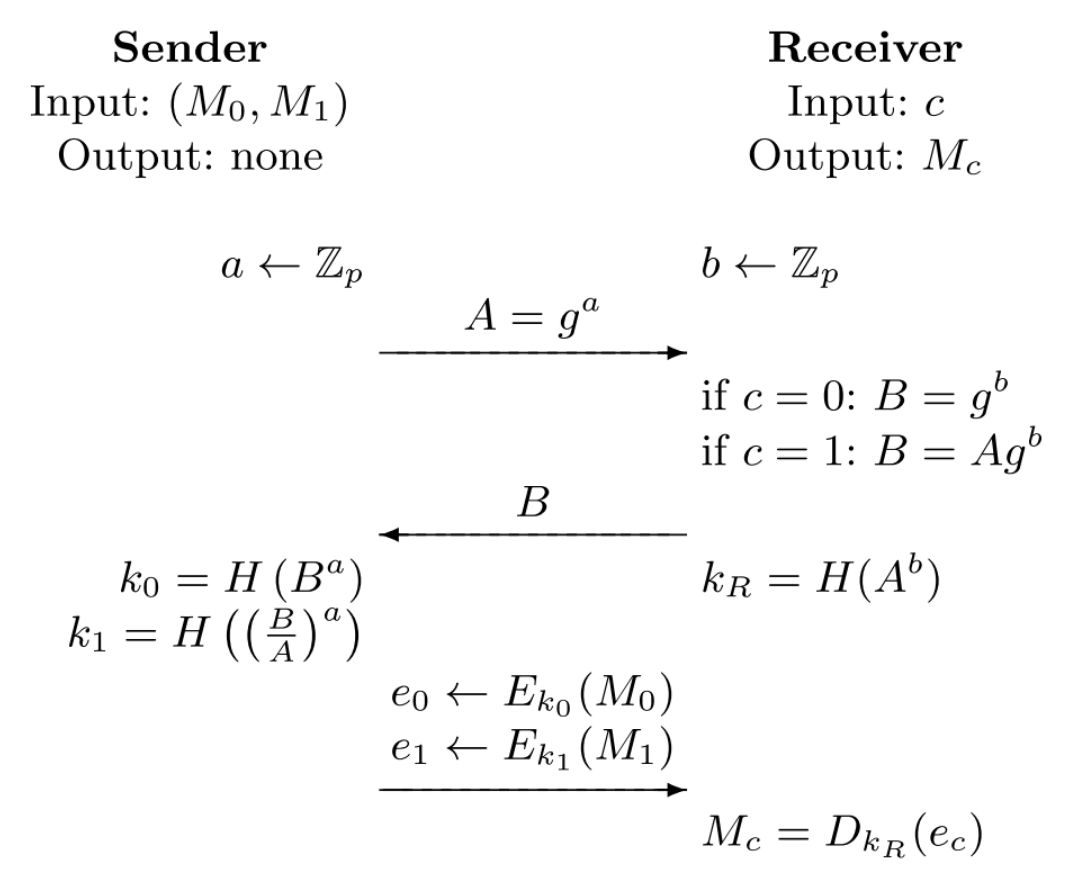
该 OT₂ 协议能够满足以下三个核心安全性质,原因如下:
-
接收方恰好获得两条消息中的一条
接收方根据自己的选择位 $c \in \{0,1\}$ 生成相应的 $B$,并最终只能够计算出与 $c$ 对应的密钥 $k_c$: 当 $c = 0$ 时,接收方能计算出 $k_0 = H(A^b) = H(B^a)$,而无法计算 $(B/A)^a$ 对应的 $k_1$;
当 $c = 1$ 时,接收方能计算出 $k_1 = H(A^b) = H((B/A)^a)$,而无法计算 $B^a$ 对应的 $k_0$。
由于计算型 Diffie–Hellman (CDH)问题的困难性,接收方在无法求解另一密钥的情况下,即使拿到另一条消息的密文 $E_{k_{1-c}}(M_{1-c})$,也无法恢复明文,从而保证他只能获得一条消息。 -
发送方不知道接收方获得的是哪一条
在步骤二中,接收方发送的 $B$ 可能是 $g^b$(当 $c = 0$)或 $A g^b$(当 $c = 1$)。对发送方来说,这两种情况的分布在随机 $b$ 的情况下是不可区分的,因为区分它们需要解决离散对数问题或CDH问题。因此,发送方只能生成两组密钥 $(k_0, k_1)$ 并分别加密两条消息,但无法判断接收方最终使用的是哪一个密钥,从而保证选择的隐私性。 -
发送方作弊可被接收方至少一半概率检测到
若发送方不按协议生成密钥或密文,试图构造特殊的 $(e_0, e_1)$ 以推测接收方的选择 $c$,接收方在解密并验证消息时会发现异常。由于接收方的选择位 $c$ 是随机的,发送方即使试图作弊,也至多有 $1/2$ 的概率猜对 $c$ 而不被发现,因此接收方有至少 50% 的概率检测到发送方的恶意行为。
3.2 随机n选一不经意传输协议的构造
在前面我们基于DH密钥协商构造了一个二选一OT协议。 下面进一步将该思想推广,提出了一个随机 n选一 OT协议,依然是在 DH 密钥协商的框架上进行改造。
-
协议目标
发送方拥有 m 组消息 $ \{ M_0^i, M_1^i, \cdots, M_{n-1}^i \}_{i=1}^m $, 其中每组有 n 条消息。接收方在每一组中选择一个索引 $l = c_i \in [n]$,并只获得该索引对应的消息 $M_l^i$,对同组的其他消息一无所知。- 协议需要满足的性质:
- 接收方只能获得所选索引的那一条消息;
- 发送方不知道接收方选择的索引;
- 支持批量执行 $m$ 次 OT。
- 协议需要满足的性质:
-
标准 n选一OT协议
- 发送方选取随机数 $y$,计算 $S = yB$ 和 $T = yS$,并发送 $S$ 给接收方。
- 接收方对于每个 OT 实例 $i$ 都选取随机数 $x_i$ 和选择索引 $c_i$,构造: $R_i = c_i S + x_i B$ 并将其转发给发送方。其中 $c_i$ 表示我将接收该 OT 实例中的第 $c_i$ 条消息 $M_{c_i}^i$。
- 发送方收到 $R_i$ 后,为每个 $j \in [n]$ 计算对称加密密钥 $k_j^i = H(S, R_i)\big(y R_i - jT\big)$ 和使用该密钥加密的密文 $e^i_j \leftarrow E(k^i_j, M^i_j)$ 并把密文集合 $\{e_j^i\}_{j=1}^n$ 发送给接收方。
- 接收方计算自己选择接收消息对应的密钥 $k^i_R = H(S, R_i)(x_i S)$ 并解密得 $M_j^i = D(e_j^i)$。
------------------------------------------------------------------------- 发送方 S 接收方 R ------------------------------------------------------------------------- (1) 选择随机 y ∈ Z_p 计算: S = y · B T = y · S 发送 S ----------------------------------> (2) 选择索引 c_i ∈ {0,1,...,n-1} 选择随机 x_i ∈ Z_p 发送 R_i 计算:R_i = c_i · S + x_i · B <--------------------------------- (3) 接收 R_i,针对每个 j ∈ {0,...,n-1}: 计算密钥并用 K_ij 加密消息: K_ij = H(S, R_i) ( y · R_i − j · T ) e_ij = E(K_ij, M^i_j) 发送 ( e_i0, ..., e_i(n−1) ) -----------------------------------> (4) 计算接收密钥: K^R_i = H(S, R_i) ( x_i · S ) 当 j = c_i 时,有: y · R_i − c_i · T = x_i · S 因此:K^R_i = K_i(c_i) 解密得到: M^i_{c_i} = D(K^R_i, e_i(c_i)) -------------------------------------------------------------------------OT 并行:对 $i = 1,\cdots,m$ 并行重复步骤 (2)–(4) 即可完成 $m$ 个 OT 实例的传输。由于这些实例可以在同一轮交互中同时发送对应的 $R_i$ 和密文集合 ${ e^i_j }$,因此整个批量执行的通信轮数与单次 OT 相同,仍是常数轮。这样接收方在一轮通信中即可获得所需的 $[ M^1_{c_1}, M^2_{c_2}, …, M^m_{c_m} ]$。
计算开销:发送方:一次性计算 $S = y \cdot B$ 和 $T = y \cdot S$ 各一次,共 $2$ 次;之后每个 OT 实例需要计算一次 $y \cdot R_i$(其余密钥通过加法得到),所以是 $m$ 次,总计 $2 + m$ 次。
接收方:每个 OT 实例需要计算一次 $x_i \cdot B$ (生成 $R_i$) 和 $x_i \cdot S$ (得到解密密钥),共 $2m$ 次。通信开销:群元素:发送方在设置阶段发送一次 $S$($1$ 个群元素),接收方在每个实例发送一个 $R_i$($m$ 个群元素),所以总计 $m + 1$ 个群元素。
密文:每个实例有 $n$ 条消息,每条消息的加密输出包含两个独立的密文单元(例如掩码和标签),所以是 $2n$ 个密文单元;$m$ 个实例共 $2mn$ 个密文单元。 -
协议能够满足目标中的性质,原因如下:
-
接收方只能获得所选索引的一条消息:接收方在每个 OT 实例中只能计算出与自己选择索引 $c_i$ 对应的密钥 $k_{c_i}^i$,接收方即使拿到所有密文 $\{ e_j^i \}_{j=1}^n$,也无法解密出非所选消息的明文。
这是因为,我们在上面提到的,发送方计算密钥的公式为 $\big(y R_i - jT\big)$ ,将其展开可得: $$ y R_i - j T = y(c_i S + x_i B) - j T = y x_i B + (c_i - j) T $$ 如果接收者选择接收的消息索引 $c_i = j$,那么上式中的 $(c_i - j) T = 0$,因此发送方计算的第 j 个密钥 $k_j^i = H(S, R_i)(x_i S) = k_R^i$ 。其他密钥由于随机项 T 的干扰导致 $k_j^i \neq k_R^i$ 。
-
发送方不知道接收方选择的索引:接收方发送的 $R_i = c_i S + x_i B$ 在不同 $c_i$ 下的分布在随机 $x_i$ 的条件下不可区分,区分它们等价于解决离散对数问题。因此,发送方只能生成并发送全部 $n$ 条消息的密文,无法判断接收方实际解密了哪一条。
-
支持批量执行 $m$ 次 OT:协议的设置阶段(发送 $S$)只需执行一次,之后可并行处理多个 OT 实例,每个实例独立生成 $R_i$、密钥和密文,从而高效地完成 $m$ 组 OT 操作。
-